Math 90: Week 5

A few administrative notes before we review the day’s material: I will not be holding office hours this Wednesday. And there are no classes next Monday, when my usual set of office hours are. But I’ve decided to do a sort of experiment: I don’t plan on reviewing for the exam specifically next week, but a large portion of the class has said that they would come to office hours on Monday if I were to have them. So I’m going to hold them to that – I’ll be in Kassar House 105 (the MRC room) from 7-8:30 (or so, later perhaps if there are a lot of questions), and this will dually function as my office hours and a sort of review session.

But this comes with a few strings attached: firstly, I’ll be willing to answer any question, but I’m not going to prepare a review; secondly, if there is poor turnout, then this won’t happen again. Alrighty!

The rest is after the fold –

The topic of the day was differentiation! The three questions of the day were –

Differentiate the following functions:
1. $e^x$
2. $e^{e^x}$
3. $e^{e^{e^x}}$
4. $\sin x$
5. $\sin (\sin x)$
6. $\sin (\sin (\sin x))$
A particle moves along a line with its position described by the function $s(t) = a_0t^2 + a_1t + a_2$ . If we know that it’s acceleration is always $20$ m/s/s, that its velocity at $t = 1$ is $-10$ m/s, and its position at $t = 2$ is $20$ m. What are $a_0, a_1, a_2$ ?
Given that , what are the following:
1. $\frac{d}{dx} (u(x))^2$
2. $\frac{d}{dx} (u(x))^n$
3. $\frac{d}{dx} (5 + x^3)^{-3}$
4. $\frac{d}{dx} ((u(x))^n)^m$

Question 1

This is all about the chain rule. Please note that this is a big deal, so if you have any trouble at all with the chain rule, seek extra help. The derivative of $e^x$ is $e^x$ . To compute the derivative of $e^{e^x}$ , we might think of $u(x) = e^x$ , so that we have $e^u$ . The derivative of $e^u$ will be $e^u u'$ , which gives us $e^{e^x}e^x$ . Let’s look at the other way of understanding the chain rule to compute the derivative of $e^{e^{e^x}}$ . The “outer function” is $e^{(\cdot)}$ . It’s derivative is just itself. The first “inner function” is $e^{e^x}$ . We have just computed its derivative above (it’s $e^{e^x} e^x$ ). So we multiply them together to get $e^{e^{e^x}}e^{e^x}e^x$ .

Similarly, the derivative of $\sin x$ is $\cos x$. The derivative of $\sin \sin x$ requires the chain rule. On the one hand, the outer function is $\sin$ , and the derivative of $\sin$ is $\cos$. So we know we will have a $\cos (\sin x)$ in the answer. The inner function is also $\sin x$ , so we need to multiply by its derivative. The final answer will be $\cos (\sin x )\cos x$ . To compute the derivative of $\sin \sin \sin x$ , we again use the chain rule. I will again use helper functions, to illustrate their use. We might call $u(x) = \sin \sin x$ , so that we are computing the derivative of $\sin (u)$ . Then we get $\cos u u'$ . We happen to have computed $u'$ just a moment ago, so the final answer is $\cos \sin \sin x \cos \sin x \sin x$ .

Question 2

The key idea of this question is to remember that the function $s(t)$ gives position at time $t$ . So its derivative gives a result in terms of position per time, the velocity. And the derivative of velocity will give a result in terms of position per time per time, or acceleration. So the velocity of our particle is $2a_0t + a_1$ , and the acceleration is $2a_0$ . Since we know that the acceleration is always $20$ , we know that $2a_0 = 20$ so that $a_0 = 10$ . The velocity at $t = 1$ is $-10$ , so we know that $2(10)(1) + a_1 = -10$ , so that $a_1 = -30$ . Finally, our position at time $t = 2$ is $20$ , so that $4(10) + 2(-30) + a_2 = 20$ , so that $a_2 = 40$ . I used different numbers between the two classes, so don’t pay too much attention if the exact details are different between one class and the other.

Question 3

This is more about the chain-rule! This is sort of an explicit example of helper functions. We first want to compute the derivative of $u(x)^2$ . By the chain rule, this will be $2u(x)u'(x)$ . What is $u'(x)$ ?. It’s $2x + 1$ . So the derivative of $u(x)^2$ is $2(x^2 + x + 2)(2x + 1)$ . This is a single case of the slightly more general $u(x)^n$ . Here, the power rule tells us that the derivative will be $nu(x)^{n-1}u'(x)$ , which is $n (x^2 + x + 2)^{n-1}(2x + 1)$ .

The idea behind the third question is to see if we can work out the same sort of idea, but without starting with a helper function. (It’s perfectly fine to always use helper functions to use the chain rule – that’s not a problem at all). The derivative of $(5 + x^3)^{-3}$ will be $-3(5 + x^3)^{-4}(3x^2)$ . If we want to see the use of helper functions, call $v(x) = 5 + x^3$ , so that we are computing the derivative of $v^{-3}$ . The derivative will be $-3v^{-4}v'$ , which is exactly what we have above.

I look forward to seeing some of you on Monday, and happy studying!

3 Responses to Math 90: Week 5

student says:

2012/10/09 at 1:31 pm

I’m writing on behalf of a emailed question that I feel might be appropriate for more people to see:

This comes in two parts.
1. Firstly, why is it that if we calculate the points of continuity of $\dfrac{x\tan x}{x^2 + 1}$ , we only end up worrying about when $\tan x$ is continuous?
2. Secondly, the book has a question about finding the discontinuities of $\csc (2x)$ , but I disagree with the book’s answer.
- mixedmath says:
  
  2012/10/09 at 1:38 pm
  
  Let’s find the points of continuity of $\csc(2x)$ . We know that $\csc(2x) = \dfrac{1}{\sin 2x}$ , so we are wondering about when $\sin (2x) = 0$
  
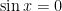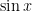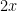  To do this, we first need to remember when $\sin x = 0$ . The zeroes of $\sin x$ are $x = 0, \pm \pi, \pm 2 \pi, ...$ or $x = n \pi$ for any integer $n$ (this includes $\sin \pi = 0$ , which you mentioned in your email). But we now have $2x$ instead of $latex $, so we might ask ourselves when 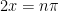$2x = n \pi$ for any integer $n$ . This happens when $x = \dfrac{n \pi}{2}$ .
  
  Let’s check ourselves – $\sin (2 \frac{n \pi}{2}) = \sin (n \pi) = 0$ . So this seems about right.
  
- mixedmath says:
  
  2012/10/09 at 1:49 pm
  
  You ask: why do we only care about when $\tan x$ is continuous when we consider $\dfrac{x \tan x}{x^2 + 1}$ ? To answer this, we need to remember something from the book:
  
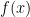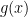  If $f(x)$ and $g(x)$ are both continuous at a point $x = c$ , then their product $f(x)g(x)$ is also continuous at the point $x = c$ .
  
  For our problem, we might realize that $\dfrac{x}{x^2 + 1}$ is continuous everywhere, but $\tan x$ is only continuous whenever $x \neq \frac{\pi}{2} + \pi n$ for any integer $n$ . This means that their product $\dfrac{x \tan x}{x^2 + 1}$ is continuous at least when both $\tan x$ and $\dfrac{x}{x^2 + 1}$ are continuous. So our function is continuous at least when $x \neq \frac{pi}{2} + \pi n$ .
  
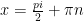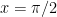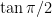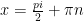  But what about when $x = \frac{pi}{2} + \pi n$ ? Let’s look at one in particular: say $x = \pi/2$ . $\tan \pi/2$ is not defined (the left limit is $+ \infty$ , the right limit is $- \infty$ , but $\tan x$ has a vertical asymptote there). In fact, $\tan x$ isn’t defined at any of these points $x = \frac{pi}{2} + \pi n$ , so these points are not in the domain of our function. So the function can’t be continuous there.
  
  So the discontinuities of $\dfrac{x \tan x}{x^2 + 1}$ are exactly the places where $\tan x$ is discontinuous.
  
  During my office hours, I mentioned that this not because of anything particularly special about $\dfrac{x}{x^2 + 1}$ , but simply because $\dfrac{x}{x^2 + 1}$ is continuous. In a sense, multiplying by a continuous function never reduces the points of continuity.

	Benjamin Chen on Hurwitz Zeta is a sum of Diric…
	shreya on A MSE Collection: Topology Boo…
	Anonymous on Are the calculus MOOCs any…
	el profe sami on Precalculus Supplement: Synthe…
	leila on An intuitive overview of Taylo…

mixedmath