This post picks up from the previous post on Summer@Brown number theory from 2013.
Now that we’d established ideas about solving the modular equation  , solving the linear diophantine equation
, solving the linear diophantine equation  , and about general modular arithmetic, we began to explore systems of modular equations. That is, we began to look at equations like
, and about general modular arithmetic, we began to explore systems of modular equations. That is, we began to look at equations like
Suppose  satisfies the following three modular equations (rather, the following system of linear congruences):
satisfies the following three modular equations (rather, the following system of linear congruences):



Can we find out what  is? This is a clear parallel to solving systems of linear equations, as is usually done in algebra I or II in secondary school. A common way to solve systems of linear equations is to solve for a variable and substitute it into the next equation. We can do something similar here.
is? This is a clear parallel to solving systems of linear equations, as is usually done in algebra I or II in secondary school. A common way to solve systems of linear equations is to solve for a variable and substitute it into the next equation. We can do something similar here.
From the first equation, we know that  for some
for some  . Substituting this into the second equation, we get that
. Substituting this into the second equation, we get that  , or that
, or that  . So
. So  will be the modular inverse of
will be the modular inverse of  . A quick calculation (or a slightly less quick Euclidean algorithm in the general case) shows that the inverse is
. A quick calculation (or a slightly less quick Euclidean algorithm in the general case) shows that the inverse is  . Multiplying both sides by
. Multiplying both sides by  yields
yields  , or rather that
, or rather that  for some
for some 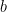 . Back substituting, we see that this means that
. Back substituting, we see that this means that  , or that
, or that  .
.
Now we repeat this work, using the third equation.  , so that
, so that  . Another quick calculation (or Euclidean algorithm) shows that this means
. Another quick calculation (or Euclidean algorithm) shows that this means  , or rather
, or rather  for some
for some  . Putting this back into
. Putting this back into  yields the final answer:
yields the final answer:


And if you go back and check, you can see that this works. 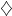
There is another, very slick, method as well. This was a clever solution mentioned in class. The idea is to construct a solution directly. The way we’re going to do this is to set up a sum, where each part only contributes to one of the three modular equations. In particular, note that if we take something like ![7 \cdot 9 \cdot [7\cdot9]_5^{-1}](https://s0.wp.com/latex.php?latex=7+%5Ccdot+9+%5Ccdot+%5B7%5Ccdot9%5D_5%5E%7B-1%7D&bg=ffffff&fg=000000&s=0&c=20201002) , where this inverse means the modular inverse with respect to
, where this inverse means the modular inverse with respect to  , then this vanishes mod
, then this vanishes mod 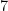 and mod
and mod  , but gives
, but gives  . Similarly
. Similarly ![2\cdot 5 \cdot 9 \cdot [5\cdot9]_7^{-1}](https://s0.wp.com/latex.php?latex=2%5Ccdot+5+%5Ccdot+9+%5Ccdot+%5B5%5Ccdot9%5D_7%5E%7B-1%7D&bg=ffffff&fg=000000&s=0&c=20201002) vanishes mod 5 and mod 9 but leaves the right remainder mod 2, and
vanishes mod 5 and mod 9 but leaves the right remainder mod 2, and ![5 \cdot 7 \cdot [5\cdot 7]_9^{-1}](https://s0.wp.com/latex.php?latex=5+%5Ccdot+7+%5Ccdot+%5B5%5Ccdot+7%5D_9%5E%7B-1%7D&bg=ffffff&fg=000000&s=0&c=20201002) vanishes mod 5 and mod 7, but leaves the right remainder mod 9.
vanishes mod 5 and mod 7, but leaves the right remainder mod 9.
Summing them together yields a solution (Do you see why?). The really nice thing about this algorithm to get the solution is that is parallelizes really well, meaning that you can give different computers separate problems, and then combine the things together to get the final answer. This is going to come up again later in this post.
These are two solutions that follow along the idea of the Chinese Remainder Theorem (CRT), which in general says that as long as the moduli are relative prime, then the system


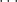

will always have a unique solution  . Note, this is two statements: there is a solution (statement 1), and the statement is unique up to modding by the product of this moduli (statement 2). Proof Sketch: Either of the two methods described above to solve that problem can lead to a proof here. But there is one big step that makes such a proof much easier. Once you’ve shown that the CRT is true for a system of two congruences (effectively meaning you can replace them by one congruence), this means that you can use induction. You can reduce the n+1st case to the nth case using your newfound knowledge of how to combine two equations into one. Then the inductive hypothesis carries out the proof.
. Note, this is two statements: there is a solution (statement 1), and the statement is unique up to modding by the product of this moduli (statement 2). Proof Sketch: Either of the two methods described above to solve that problem can lead to a proof here. But there is one big step that makes such a proof much easier. Once you’ve shown that the CRT is true for a system of two congruences (effectively meaning you can replace them by one congruence), this means that you can use induction. You can reduce the n+1st case to the nth case using your newfound knowledge of how to combine two equations into one. Then the inductive hypothesis carries out the proof.
Note also that it’s pretty easy to go backwards. If I know that  , then I know that
, then I know that  will also be the solution to the system
will also be the solution to the system


In fact, a higher view of the CRT reveals that the great strength is that considering a number mod a set of relatively prime moduli is the exact same (isomorphic to) considering a number mod the product of the moduli.
The remainder of this post will be about why the CRT is cool and useful.
Application 1: Multiplying Large Numbers
Firstly, the easier application. Suppose you have two really large integers  (by really large, I mean with tens or hundreds of digits at least – for concreteness, say they each have
(by really large, I mean with tens or hundreds of digits at least – for concreteness, say they each have  digits). When a computer computes their product
digits). When a computer computes their product  , it has to perform
, it has to perform 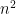 digit multiplications, which can be a whole lot if
digit multiplications, which can be a whole lot if  is big. But a computer can calculate mods of numbers in something like
is big. But a computer can calculate mods of numbers in something like  time, which is much much much faster. So one way to quickly compute the product of two really large numbers is to use the Chinese Remainder Theorem to represent each of
time, which is much much much faster. So one way to quickly compute the product of two really large numbers is to use the Chinese Remainder Theorem to represent each of  and
and 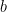 with a set of much smaller congruences. For example (though we’ll be using small numbers), say we want to multiply
with a set of much smaller congruences. For example (though we’ll be using small numbers), say we want to multiply  by
by 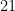 . We might represent
. We might represent  by
by  and represent
and represent 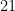 by
by  . To find their product, calculate their product in each of the moduli:
. To find their product, calculate their product in each of the moduli:  . We know we can get a solution to the resulting system of congruences using the above algorithm, and the smallest positive solution will be the actual product.
. We know we can get a solution to the resulting system of congruences using the above algorithm, and the smallest positive solution will be the actual product.
This might not feel faster, but for much larger numbers, it really is. As an aside, here’s one way to make it play nice for parallel processing (which vastly makes things faster). After you’ve computed the congruences of  and
and 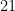 for the different moduli, send the numbers mod 5 to one computer, the numbers mod 7 to another, and the numbers mod 11 to a third (but also send each computer the list of moduli: 5,7,11). Each computer will calculate the product in their modulus and then use the Euclidean algorithm to calculate the inverse of the product of the other two moduli, and multiply these together. Afterwards, the computers resend their data to a central computer, which just adds the result and takes it mod
for the different moduli, send the numbers mod 5 to one computer, the numbers mod 7 to another, and the numbers mod 11 to a third (but also send each computer the list of moduli: 5,7,11). Each computer will calculate the product in their modulus and then use the Euclidean algorithm to calculate the inverse of the product of the other two moduli, and multiply these together. Afterwards, the computers resend their data to a central computer, which just adds the result and takes it mod  (to get the smallest positive solution). Since mods are fast and all the multiplication is with smaller integers (no bigger than the largest mod, ever), it all goes faster. And since it’s parallelized, you’re replacing a hard task with a bunch of smaller easier tasks that can all be worked on at the same time. Very powerful stuff!
(to get the smallest positive solution). Since mods are fast and all the multiplication is with smaller integers (no bigger than the largest mod, ever), it all goes faster. And since it’s parallelized, you’re replacing a hard task with a bunch of smaller easier tasks that can all be worked on at the same time. Very powerful stuff!
I have actually never seen someone give the optimal running time that would come from this sort of procedure, though I don’t know why. Perhaps I’ll look into that one day.
Application 2: Secret Sharing in Networks of People
This is really slick. Let’s lay out the situation: I have a secret. I want you, my students, to have access to the secret, but only if at least six of you decide together that you want access. So I give each of you a message, consisting of a number and a modulus. Using the CRT, I can create a scheme where if any six of you decide you want to open the message, then you can pool your six bits together to get the message. Notice, I mean any six of you, instead of a designated set of six. Further, no five people can recover the message without a sixth in a reasonable amount of time. That’s pretty slick, right?
The basic idea is for me to encode my message as a number 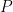 (I use P to mean plain-text). Then I choose a set of moduli, one for each of you, but I choose them in such a way that the product of any
(I use P to mean plain-text). Then I choose a set of moduli, one for each of you, but I choose them in such a way that the product of any  of them is smaller than
of them is smaller than 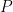 , but the product of any
, but the product of any 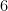 of them is greater than
of them is greater than 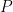 (what this means is that I choose a lot of primes or near-primes right around the same size, all right around the fifth root of
(what this means is that I choose a lot of primes or near-primes right around the same size, all right around the fifth root of 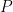 ). To each of you, I give you the value of
). To each of you, I give you the value of  and the modulus
and the modulus  , where
, where  is your modulus. Since
is your modulus. Since 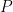 is much bigger than
is much bigger than  , it would take you a very long time to just happen across the correct multiple that reveals a message (if you ever managed). Now, once six of you get together and put your pieces together, the CRT guarantees a solution. Since the product of your six moduli will be larger than
, it would take you a very long time to just happen across the correct multiple that reveals a message (if you ever managed). Now, once six of you get together and put your pieces together, the CRT guarantees a solution. Since the product of your six moduli will be larger than 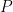 , the smallest solution will be
, the smallest solution will be 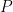 . But if only five of you get together, since the product of your moduli is less than
. But if only five of you get together, since the product of your moduli is less than 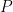 , you don’t recover
, you don’t recover 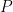 . In this way, we have our secret sharing network.
. In this way, we have our secret sharing network.
To get an idea of the security of this protocol, you might imagine if I gave each of you moduli around the size of a quadrillion. Then missing any single person means there are hundreds of trillions of reasonable multiples of your partial plain-text to check before getting to the correct multiple.
A similar idea, but which doesn’t really use the CRT, is to consider the following problem: suppose two millionaires Alice and Bob (two people of cryptological fame) want to see which of them is richer, but without revealing how much wealth they actually have. This might sound impossible, but indeed it is not! There is a way for them to establish which one is richer but with neither knowing how much money the other has. Similar problems exist for larger parties (more than just 2 people), but none is more famous than the original: Yao’s Millionaire Problem.
Alright – I’ll see you all in class.
Leave a Response »








